快速排序 & 快速选择
基准点的选取
基准点(pivot)是快速选择和快速排序算法中的一个关键概念。基准点的选取方法可以有很多种,常见的策略包括:
基准点的选取会影响算法的性能。如果每次选取的基准点都能将数组近似平分,那么快速排序的性能会更好。
逆序和正序的区别
在快速选择和快速排序算法中,逆序和正序的主要区别在于分区过程中比较和交换的方向。
正序排序
正序排序是指从小到大排序。在分区过程中,目标是将所有小于基准点的元素放在基准点的左侧,将所有大于基准点的元素放在基准点的右侧。
具体步骤如下:
- 从左向右找到第一个大于等于基准点的元素。
- 从右向左找到第一个小于等于基准点的元素。
- 交换这两个元素。
- 重复上述步骤直到左右指针相遇。
逆序排序
逆序排序是指从大到小排序。在分区过程中,目标是将所有大于基准点的元素放在基准点的左侧,将所有小于基准点的元素放在基准点的右侧。
具体步骤如下:
- 从右向左找到第一个大于等于基准点的元素。
- 从左向右找到第一个小于等于基准点的元素。
- 交换这两个元素。
- 重复上述步骤直到左右指针相遇。
注意:
逆序和正序排序没有本质的区别,但是需要注意的是,如果最后基准数是被放置在了最左边,那么交换过程应该先从右边开始交换,同理,如果最后基准数是被放置在了最右边,那么交换过程应该先从左边开始交换,这一点,无论逆序和正序都是一样的。
左右指针法
public static void quickSort(int[] arr, int left, int right) {
if (left >= right) return;
int i = left, j = right;
int pivot = arr[left];
while (i < j) {
while (i < j && arr[j] >= pivot) j--;
while (i < j && arr[i] <= pivot) i++;
if (i < j) swap(arr, i, j);
}
swap(arr, left, i);
quickSort(arr, left, i - 1);
quickSort(arr, i + 1, right);
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
|
挖矿法
public static void quickSort(int[] arr, int left, int right) {
if (left >= right) return;
int i = left, j = right;
int pivot = arr[left];
while (i < j) {
while (i < j && arr[j] >= pivot) j--;
if (i < j) arr[i++] = arr[j];
while (i < j && arr[i] <= pivot) i++;
if (i < j) arr[j--] = arr[i];
}
arr[i] = pivot;
quickSort(arr, left, i - 1);
quickSort(arr, i + 1, right);
}
|
数组中第K个最大的元素
class Solution {
public int findKthLargest(int[] nums, int k) {
int ans = quickSelect(nums, 0, nums.length - 1, k - 1);
return ans;
}
public int quickSelect(int[] nums, int left, int right, int k) {
if (left >= right) {
return nums[k];
}
int mid = left + (right - left) / 2;
int pivot = nums[mid];
swap(nums, mid, right);
int l = left;
int r = right;
while (l < r) {
while (l < r && nums[l] >= pivot) {
l++;
}
while (l < r && nums[r] <= pivot) {
r--;
}
if (l < r) {
swap(nums, l, r);
}
}
swap(nums, l, right);
if (l == k) {
return nums[l];
} else if (l < k) {
return quickSelect(nums, l + 1, right, k);
} else {
return quickSelect(nums, left, l - 1, k);
}
}
public void swap(int[] nums, int l, int r) {
int t = nums[l];
nums[l] = nums[r];
nums[r] = t;
}
}
|
算法分析
1、时间复杂度
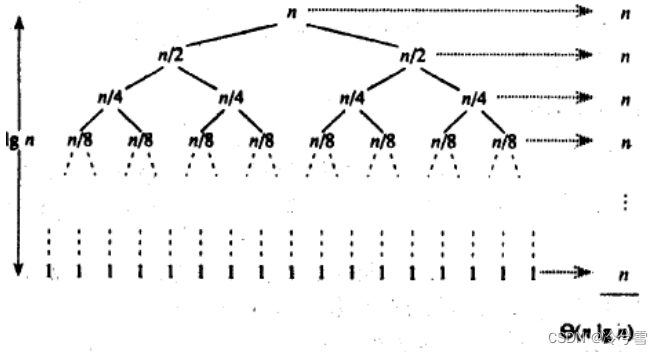
快速排序的时间复杂度为O(nlogn),其中n为待排序数组的长度。最坏情况下,快速排序的时间复杂度为O(n^2),但这种情况出现的概率很小,可以通过一些优化措施来避免。
2、空间复杂度
快速排序的空间复杂度取决于递归栈的深度,在最坏情况下,递归栈的深度为O(n),因此快速排序的空间复杂度为O(n)。但是,在一些实现中,可以使用非递归的方式来实现快速排序,从而避免递归栈带来的空间开销。
3、稳定性
快速排序是一种不稳定的排序算法。因为在排序过程中,可能会交换相同元素的位置,从而导致相同元素的相对顺序被改变。例如,对于数组[3, 2, 2, 1],如果选择第一个元素3作为基准元素,那么经过第一次划分后,数组变成了[1, 2, 2, 3],其中两个2的相对顺序被改变了。
应用场景
- 大规模数据排序:快速排序的时间复杂度为 O(nlogn),在大规模数据排序时表现优秀。
- 数据重复性较少的排序:在排序的数据中,如果存在大量重复的元素,那么快速排序的效率会受到影响,因为这样会增加比较和交换的次数。
- 对数据随机性要求不高的排序:由于快速排序的分区过程是基于一个基准元素来完成的,因此如果待排序数据的分布比较随机,那么快速排序的效率会很高。
堆排序 (优先级队列)
构建大根堆
public void buildMaxHeap(int[] nums, int heapSize) {
for (int i = heapSize / 2 - 1; i >= 0; i--) {
heapify(nums, i, heapSize);
}
}
public void heapify(int[] nums, int index, int heapSize) {
int largest = index;
int left = 2 * index + 1;
int right = 2 * index + 2;
if (left < heapSize && nums[left] > nums[largest]) {
largest = left;
}
if (right < heapSize && nums[right] > nums[largest]) {
largest = right;
}
if (largest != index) {
swap(nums, index, largest);
heapify(nums, largest, heapSize);
}
}
public void swap(int[] nums, int l, int r) {
int t = nums[l];
nums[l] = nums[r];
nums[r] = t;
}
|
构建小跟堆
public void buildMinHeap(int[] nums) {
int heapSize = nums.length;
for (int i = heapSize / 2 - 1; i >= 0; i--) {
heapify(nums, i, heapSize);
}
}
public void heapify(int[] nums, int index, int heapSize) {
int smallest = index;
int left = 2 * index + 1;
int right = 2 * index + 2;
if (left < heapSize && nums[left] < nums[smallest]) {
smallest = left;
}
if (right < heapSize && nums[right] < nums[smallest]) {
smallest = right;
}
if (smallest != index) {
swap(nums, index, smallest);
heapify(nums, smallest, heapSize);
}
}
public void swap(int[] nums, int l, int r) {
int t = nums[l];
nums[l] = nums[r];
nums[r] = t;
}
|
总结
- 堆排序使用堆来选数,相比直接选择排序效率就高了很多。堆排序中每一趟都有元素归位了
- 时间复杂度:最好/最环/平均时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
- 适用场景:元素较多的情况,因为建初始堆的所需的比较次数比较多,所有堆排序不适合元素较少的时候
数组中第K个最大的元素
class Solution {
public int findKthLargest(int[] nums, int k) {
int heapSize = nums.length;
buildMaxHeap(nums, heapSize);
for (int i = nums.length - 1; i >= nums.length - k + 1; i--) {
swap(nums, 0, i);
--heapSize;
heapify(nums, 0, heapSize);
}
return nums[0];
}
public void buildMaxHeap(int[] nums, int heapSize) {
for (int i = heapSize / 2 - 1; i >= 0; i--) {
heapify(nums, i, heapSize);
}
}
public void heapify(int[] nums, int index, int heapSize) {
int largest = index;
int left = 2 * index + 1;
int right = 2 * index + 2;
if (left < heapSize && nums[left] > nums[largest]) {
largest = left;
}
if (right < heapSize && nums[right] > nums[largest]) {
largest = right;
}
if (largest != index) {
swap(nums, index, largest);
heapify(nums, largest, heapSize);
}
}
public void swap(int[] nums, int l, int r) {
int t = nums[l];
nums[l] = nums[r];
nums[r] = t;
}
}
|
桶排序(计数排序)
public static void bucketSort(float[] arr) {
int n = arr.length;
if (n <= 0) return;
ArrayList<Float>[] buckets = new ArrayList[n];
for (int i = 0; i < n; i++) {
buckets[i] = new ArrayList<>();
}
for (int i = 0; i < n; i++) {
int bucketIndex = (int) (arr[i] * n);
buckets[bucketIndex].add(arr[i]);
}
for (int i = 0; i < n; i++) {
Collections.sort(buckets[i]);
}
int index = 0;
for (int i = 0; i < n; i++) {
for (float num : buckets[i]) {
arr[index++] = num;
}
}
}
|
总结:
典型的空间换时间,适用于数据范围不大的集合
数组中第K个最大的元素
class Solution {
public int findKthLargest(int[] nums, int k) {
int[] buckets = new int[20001];
for (int i = 0; i < nums.length; i++) {
buckets[nums[i] + 10000]++;
}
for (int i = 20000; i >= 0; i--) {
k = k - buckets[i];
if (k <= 0) {
return i - 10000;
}
}
return 0;
}
}
|




