从零开始的算法学习(三)
二叉树
class Node<V>{
V value;
Node left;
Node right;
}
|
问题一
用递归和非递归两种方式实现二叉树的先序、中序、后序遍历
如何直观的打印一颗二叉树 ?
如何完成二叉树的宽度优先遍历 ?
左右节点(孩子)都为空的节点就叫做叶子节点
递归序
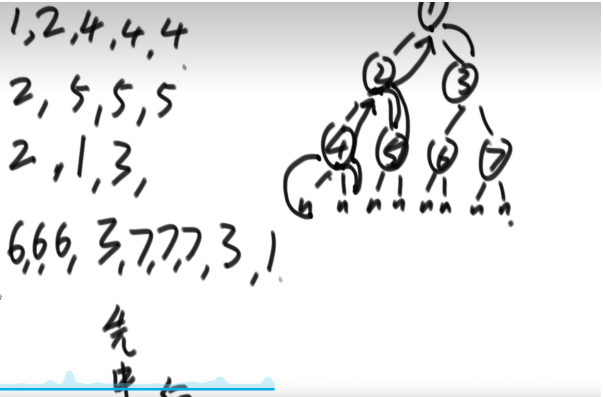
1 2 4 4 4(三次返回)2 5 5 5 2 (三次返回2)1 3 6 6 6 3 7 7 7 3 (三次返回7) 3 (三次返回3)1
在递归序的基础上,有三种遍历方式
- 先序:对于所有子树来说,都是先打印子树的头节点,在打印子树的左边节点,在打印子树的右边节点
1 2 4 5 3 6 7
第一次来到某个节点,就直接打印该节点,其他时候不打印
- 中序:对于每一颗子树,都是先打印左边节点,在打印头节点,在打印右边节点
4 2 5 1 6 3 7
第一次来到某个节点什么都不做,第二次来到某个节点打印该节点,第三次来到某个节点,什么都不做
- 后序:对于每一颗子树,都是先打印左边节点,在打印右边节点,在打印头节点
4 5 2 6 7 3 1
第一次来到某个节点什么都不做,第二次来到某个节点什么都不做,第三次来到某个节点,打印该节点
public static void preOrderRecur(Node head){
if(head == null){
return;
}
System.out.print(head.value + " ");
preOrderRecur(head.left);
preOrderRecur(head.right);
}
public static void inOrderRecur(Node head){
if(head == null){
return;
}
inOrderRecur(head.left);
System.out.print(head.left + " ");
inOrderRecur(head.right);
}
public static void postOrderRecur(Node head){
if(head == null){
return;
}
preOrderRecur(head.left);
preOrderRecur(head.right);
System.out.print(head.value + " ");
}
|
非递归实现先序遍历
- 先把头节点入栈
- 从栈中弹出一个节点记为cur
- 打印或者处理cur
- 把cur的孩子先右再左入栈(如果有的话)
- 重复以上步骤
public static void preOrderUnRecur(Node head){
System.out.print("pre-order: ");
if(head != null){
Stack<Node> stack = new Stack<>();
stack.add(head);
while (!stack.isEmpty()){
head = stack.pop();
System.out.print(head.value + " ");
if(head.right != null){
stack.push(head.right);
}
if(head.left != null){
stack.push(head.left);
}
}
}
System.out.println();
}
|
中序遍历
每棵子树整棵树的左边界进栈,依次弹出的过程中,打印,对于弹出节点的右树重复左边界入栈的操作
- 从头节点开始,每个节点的左边界(左边的全部节点,包括头节点)全部入栈
- 弹出一个节点cur,打印该节点
- 对于cur,把cur的右节点作为新的头节点,重复节点的左边界进栈
- 弹出一个节点cur,打印该节点(直到栈空)
public static void inOrderUnRecur(Node head){
System.out.println("in-order: ");
if(head != null){
Stack<Node> stack = new Stack<>();
while (!stack.isEmpty() || head != null){
if(head != null){
stack.push(head);
head = head.left;
}else {
head = stack.pop();
System.out.println(head.value + " ");
head = head.right;
}
}
}
System.out.println();
}
|
后序遍历(准备两个栈 s1 s2)
- 先把头节点入栈s1
- 从栈s1中弹出一个节点cur
- 把cur的子节点按照先左再右的顺序入栈s1
- 把cur放入栈s2
- 从栈s1中弹出一个节点cur(这一步开始重复知道s1为空)
- 按照出栈顺序打印s2栈中元素
public static void postOrderUnRecur(Node head){
if(head != null){
Stack<Node> s1 = new Stack<>();
Stack<Node> s2 = new Stack<>();
s1.push(head);
while (!s1.isEmpty()){
head = s1.pop();
if(head.left != null){
s1.push(head.left);
}
if(head.right != null){
s1.push(head.right);
}
s2.push(head);
}
while (!s2.isEmpty()){
System.out.print(s2.pop().value + " ");
}
}
}
|
对于二叉树来说
先序遍历就是二叉树的深度优先遍历
二叉树的宽度优先遍历
- 设置一个队列
- 头节点入队列
- 出队列设置为cur,并打印cur
- 对于cur,先放cur的左节点,再放cur的右节点
- 出队列设置为cur,并打印cur,对于cur, 先放左再放右(重复知道队列为空)
public static void w(Node head){
if(head == null){
return;
}
Queue<Node> queue = new LinkedList<>();
queue.add(head);
while(!queue.isEmpty()){
Node cur = queue.poll();
System.out.print(cur.value);
if(cur.left != null){
queue.add(cur.left);
}
if(cur.right != null){
queue.add(cur.right);
}
}
}
|
求一颗二叉树的最大宽度
- 定义一个HashMap用于记录每个节点在第几层
- 定义 curLevel 记录当前层数 curLevelNodes 记录当前层节点数 max 记录节点最多的层数
public static void w(Node head){
if(head == null){
return;
}
Queue<Node> queue = new LinkedList<>();
queue.add(head);
HashMap<Node, Integer> levelMap = new HashMap<>();
levelMap.put(head, 1);
int curLevel = 1;
int curLevelNodes = 0;
int max = Integer.MIN_VALUE;
while(!queue.isEmpty()){
Node cur = queue.poll();
int curNodeLevel = levelMap.get(cur);
if(curNodeLevel == curLevel){
curLevelNodes++;
}else{
max = Math.max(max, curLevelNodes);
curLevel++;
curLevelNodes = 1;
}
if(cur.left != null){
levelMap.put(cur.left, curNodeLevel+1);
queue.add(cur.left);
}
if(cur.right != null){
levelMap.put(cur.right, curNodeLevel+1);
queue.add(cur.right);
}
}
}
|

二叉树的相关概念
搜索二叉树
每一颗子树,左树都比它小,右树都比它大
判断方式:
中序遍历一颗树的节点,如果发现总是在增大,那么就是搜索二叉树
思路:
- 左树是搜索二叉树
- 右树是搜索二叉树
- 左树Max < x
- 右数Min > x
完全二叉树
判断方式:
二叉树按照宽度来遍历
- 任一节点,有右节点,没有左节点,返回false
- 在上一个条件不违规的条件下, 如果遇到了第一个左右两个孩子不双全的情况,接下来遇到的所有节点都必须是叶子节点,否则不是完全二叉树
满二叉树
判断方式:
- 统计最大深度 L
- 统计节点个数 N
- 满二叉树:N = 2^L - 1
平衡二叉树
对于每一颗子树来说,左树高度与右树的高度差都不大于 1
推断:
假设平衡二叉树的头是X
- X的左树是平衡二叉树 (是否是平衡二叉树 ?高度多少?)
- X的右树是平衡二叉树(是否是平衡二叉树 ?高度多少?)
- |左树的高度 - 右树的高度| <= 1
运用这递归套路,可以解决一切树型DP问题
什么问题不能用这种递归套路来解决呢?
不能把问题简化为用左右两边提供的信息解的题
例题
给定两个二叉树的节点node1和node2,找到他们的最低公共祖先节点
最低公共祖先:两个节点网上,最先汇聚的点
情况分析:
- o1是o2的Lca,或者 o2 是 o1的最低公共祖先
- o1和o2彼此不互为最低公共祖先
public static Node lowestAncestor(Node head, Node o1, Node o2){
if(head == null || head == o1 || head == o2){
return head;
}
Node left = lowestAncestor(head.left, o1, o2);
Node right = lowestAncestor(head.right, o1, o2);
if(left != null && right != null){
return head;
}
return left != null ? left : right;
}
|
思路:
- 如果x有右树,那么x的后继节点就是x的右树的最左的节点(如果右树没有左树,右节点就是后继节点)
- 如果x没有右树,那么x的后继节点,就是顺着x向上找,直到某个节点是其父节点的左边节点,该节点的父节点就是x的后继节点
二叉树的序列化和反序列化
序列化:
将内存中的一颗树,转换为一个字符串,并且该字符串与该树一一对应
反序列化:
根据序列化的树字符串,还原为内存中的树
折纸问题(可以理解为二叉树的中序遍历)







